자료 구조

1. Array

1.1 정의

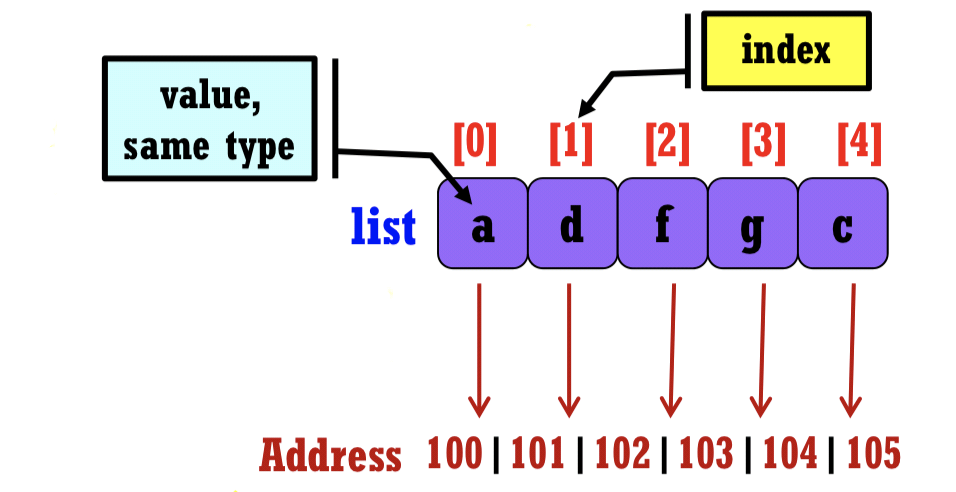
• A set of pairs, <index, value> such that each index has a value associated with it
  • 모든 값은 같은 데이터 타입을 가져야 한다.
  • 연속적 메모리 공간에 allocation 됨
  • 메모리 사이즈가 정해지면, 런타임 동안에는 수정 불가

  

1.2 특징

• Sequential representation
  • 메모리 상에 연속적으로 선언되어 있음
• Insert & Delete : Inefficient due to data shift - O(n)
  • 데이터를 array 중간에 넣거나 삭제하려면, 나머지 데이터의 이동이 발생하여 비효율 적
• Size of data must be predefined
  • 메모리 상에 연속적으로 선언되어야 하므로, array의 크기는 compile time에 미리 선언되어야 함
• Static storage allocation
  • 앞과 같은 이유로 프로그램 수행 도중에 사이즈를 바꿀 수 없음

1.3 Operator & Time Complexity

• Retrieve(A, i) : array A에 i-index의 값을 가져오기
• Store(A, i, X) : array A에 i-index에 X값을 넣음
  • 위 두개의 operator는 index가 메모리에 위치적으로 연속하기 때문에 direct access가능!, time complexity O(1)

• Insert(A, i, X): array A의 i-index에 X값을 삽입
  • 위의 Store와 다르게, 뒤쪽에 있는 데이터를 한칸씩 밀어야함
  • 비효율적! O(n)

• Delete(A, i) : array A의 i-index의 값을 삭제하고 뒤에 있는 데이터를 당김
  • data movement 발생!
  • 비효울적! O(n)

1.4 2-Dimensional array

• m & n 의 row, column 테이블이 표현하고 싶을 때 2차원 array 필요

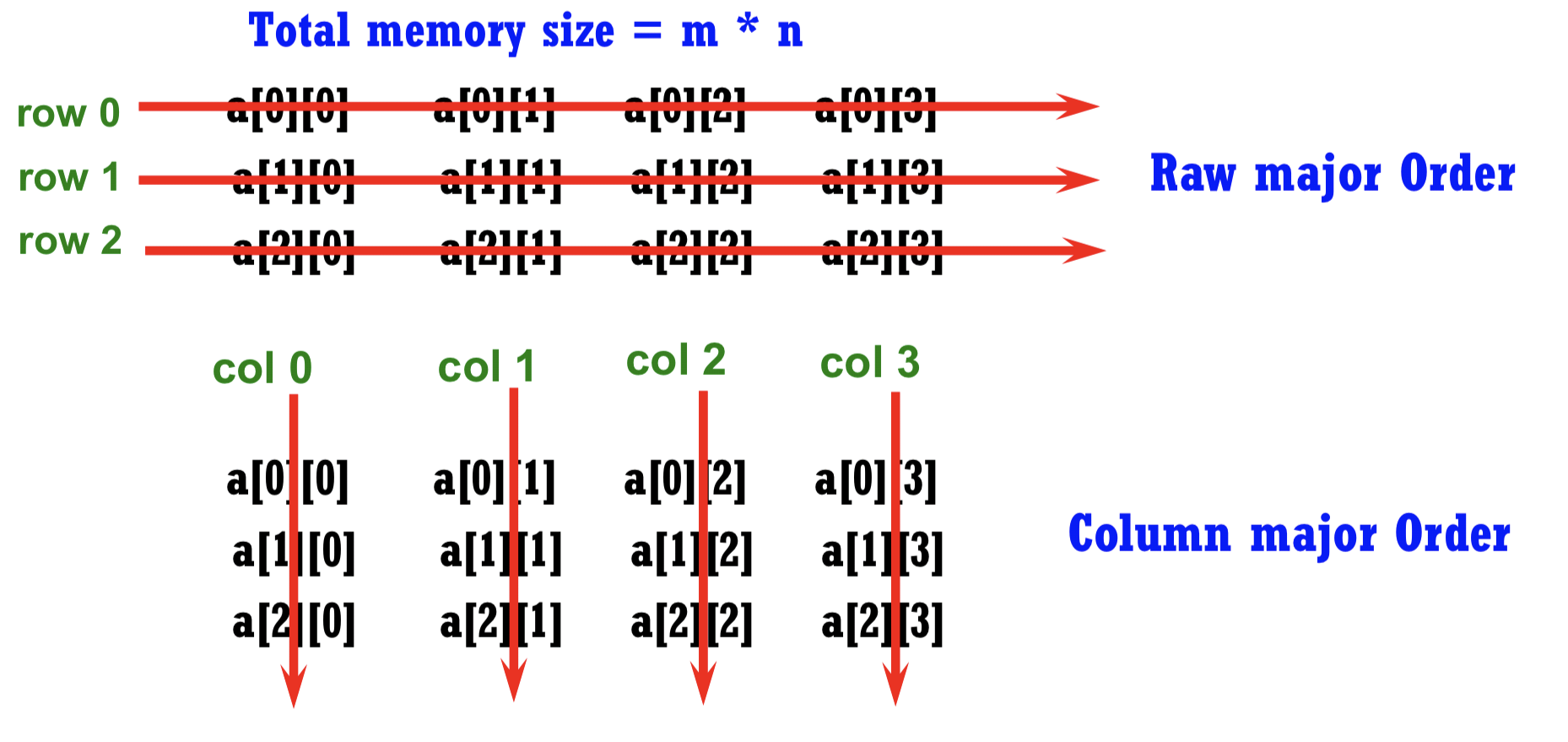
• 대부분의 element가 0인 경우 Sparse Matrix 사용을 고려
  • Sparse Matrix : 2-D array -> <row index, column index, non-zero value>

2. Stack

2.1 정의

• A list whose end points are pointed by top and bottom
  • 양 마지막 부분이 top과 bottom으로 point된 리스트
• Insertion and deletion take place at the top
  • top부분에서만 삽입과 삭제가 이루어진다.
• Bottom is constant, but top grow and shrinks
• Not possibple to access the items within stack, except top!
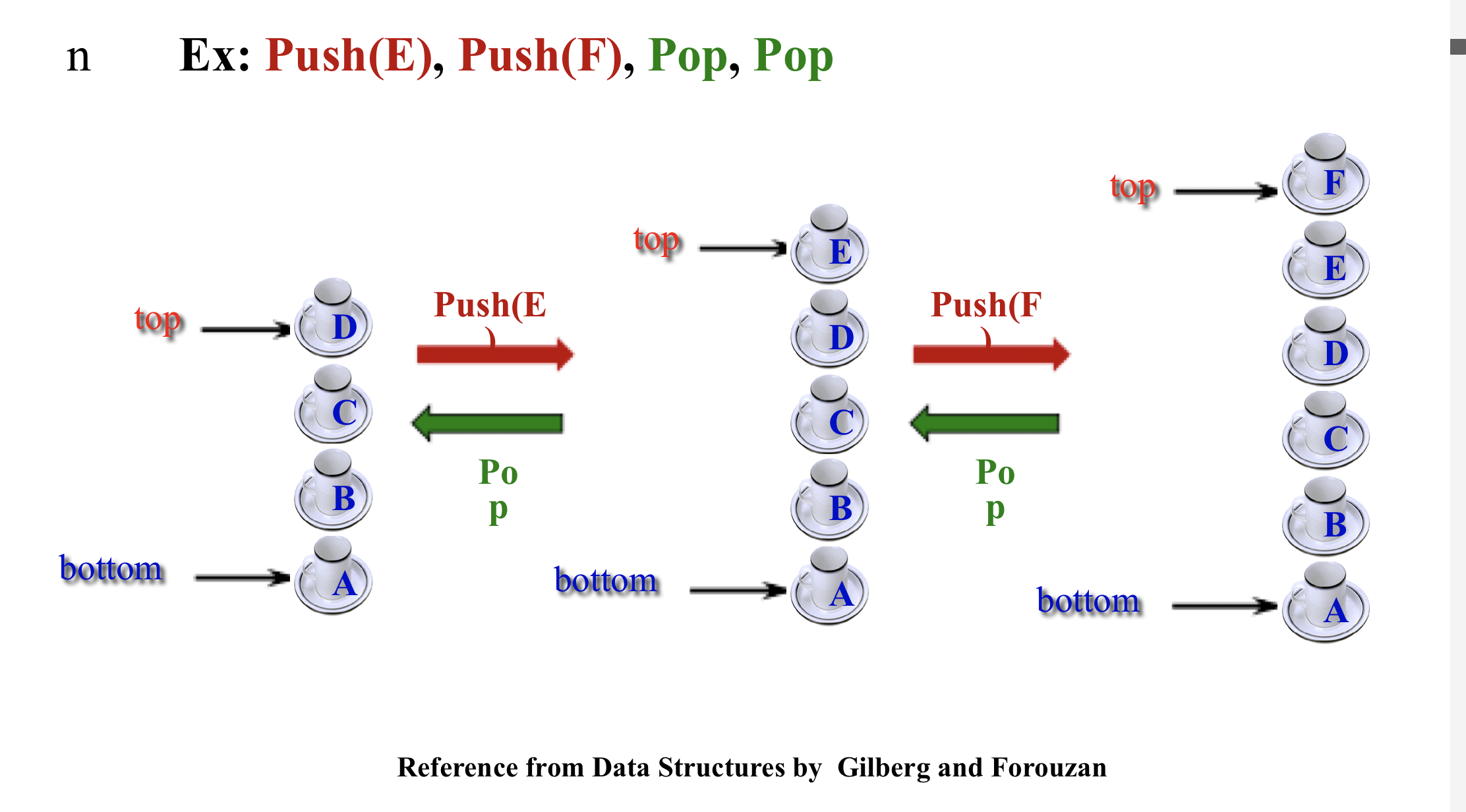
• LIFO (Last-In First-Out)

2.2 Implementation : Use of array

• Use one-dimensional Array
• Use one variable : top
• Always initialize the top by -1

2.2.1 Operators : Push and pop

• Push : Insert an item into a stack

  void push (int top, element item){
  if(top >= MAX_STACK_SIZE -1) return stack_full();
  top = top + 1;
  stack[top] = item;
  }
  

• Pop : Delete an item from a stack

  element pop(int top){
  if (top == -1) return stack_empty();
  item = stack[top];
  top = top -1;
  }
  

2.3 Stack의 활용

• Evaluation of Arithmetic Expressions
• Maze Problem
• Parsing (Pattern Matching)
• Function Calls/Returns
• Queens Problem
• Backtracking

3. Queue

3.1 정의

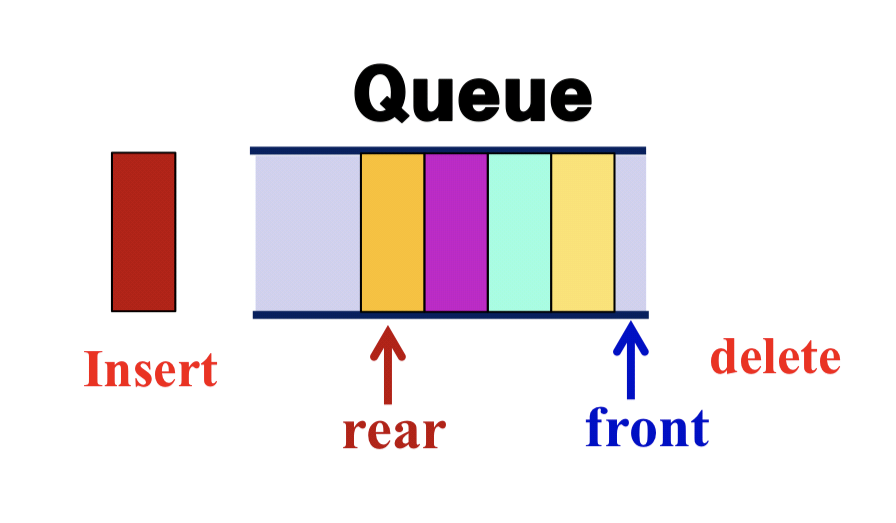
• A list whose ends are pointed by front and rear
  • stack과 비슷하면서도 다름
• Insertion and deletion take place at rear and front, repectively
  • stack과 다른 점
• Not possible to acceess all items except front and rear
  • stack은 top만 접근 가능
• FIFO (First-In First-Out)

3.2 Implementaion : Use of Array

• Use one-dimensional array
• Use two variables : front, rear
• Initialize always both front and rear by -1

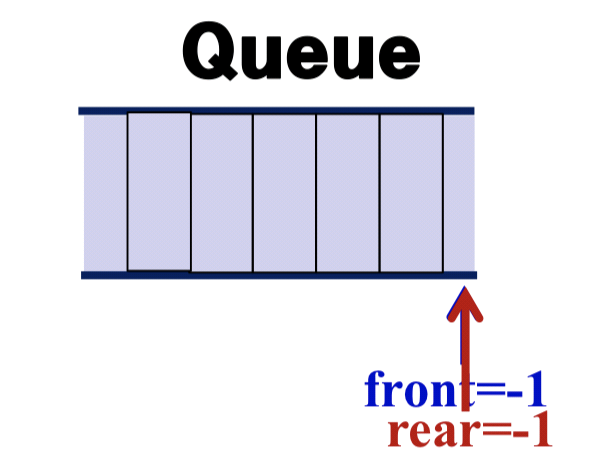
3.2.1 Operators : Insert / Delete

• Insert

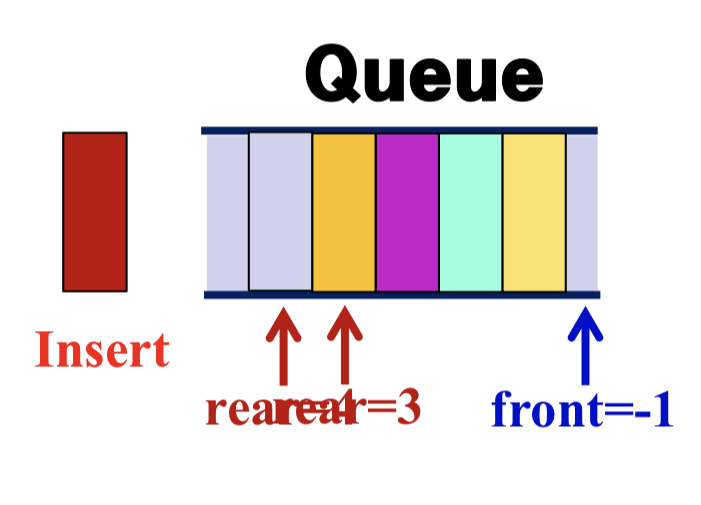
  Insert(element item){
  if (rear == MAX_Q_SIZE-1) return queue_full();
  rear = rear + 1;
  queue[rear] = item;
  }
  

• Delete

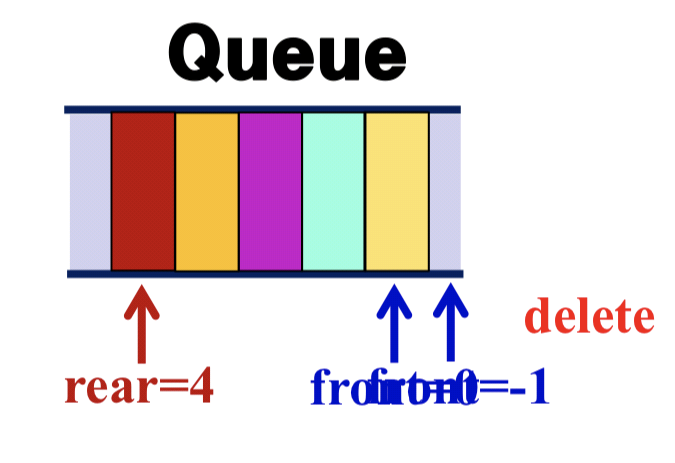
  Delete(){
  if (front == rear) return queue_empty();
  front = front + 1;
  item = queue[front];
  }
  

3.3 Problems

• Queue always moves to the right direction.
• Queue_full(i.e., rear == MAX_Q_SIZE - 1) condition does not always mean that there are maximum items in queue
  • front가 delete() 가 call 될 때마다 +1 되므로, array의 앞부분이 버려진 채로 남게 된다.
• There still may be empty spaces available even if queue is full.
• If you wnat to insert an item, all data should be moved!
  • In the worst case, O(n) - Inefficient
• Solution - Circular Queue

3.4 Circular Queue

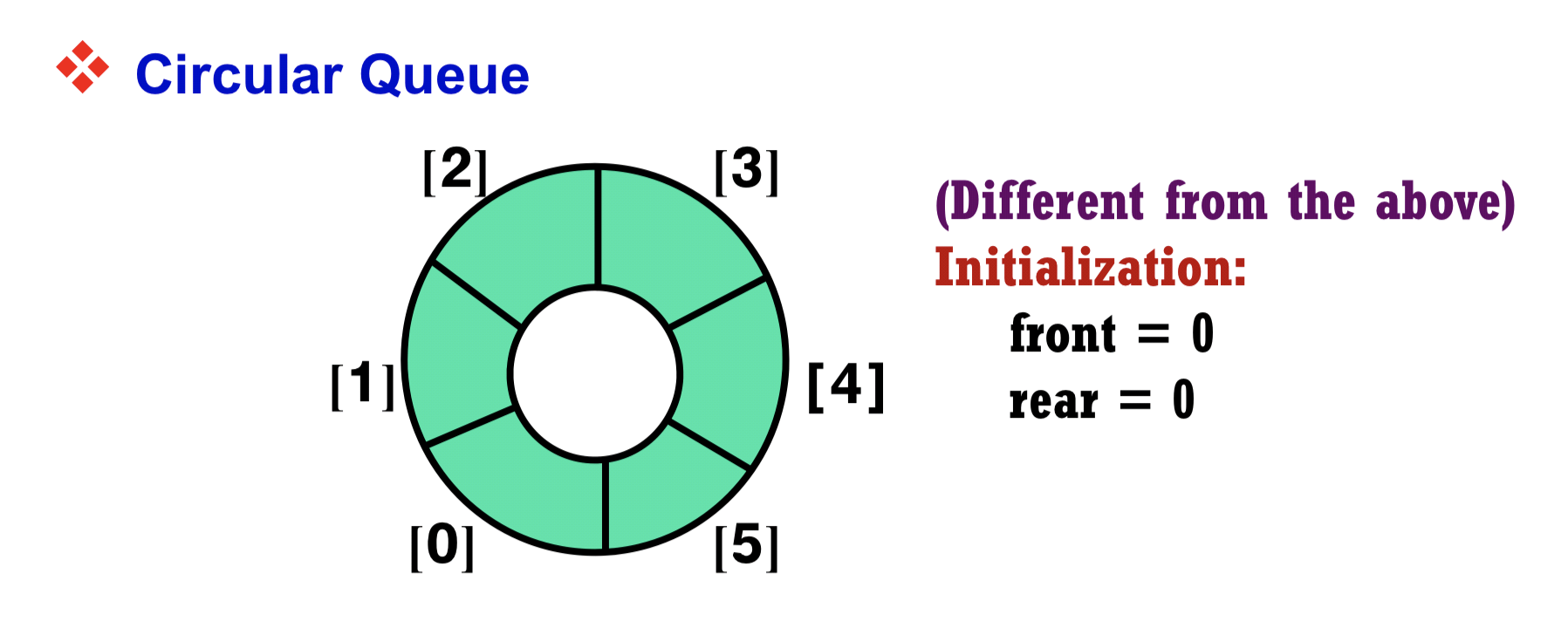
• front + 1 is the same as the actual front value
• rear is the same as the actual rear value

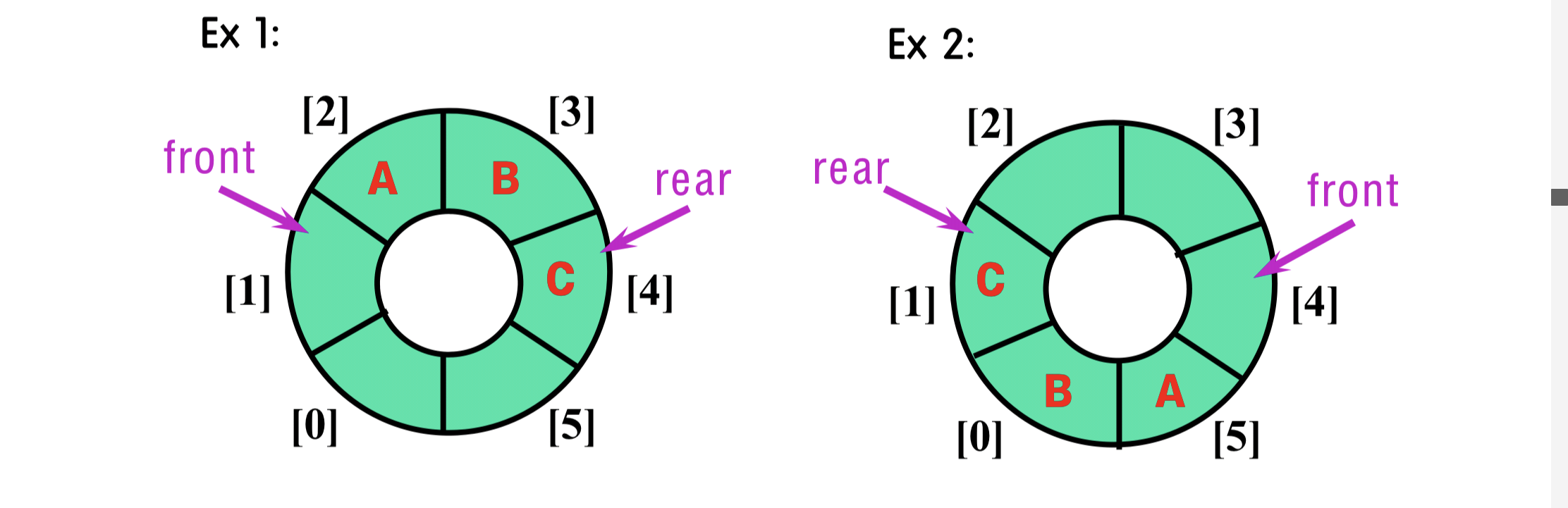
3.4.1 Operator

• Insert
  • Increment “rear” by “1” in a clockwise direction;
  • if “rear” reaches the end of queue, reset “rear” by “0”
  • Queue Full Condition : front == rear

    Insert(element item){
    rear = (rear + 1) % MAX_Q_SIZE  ///Circluar !
    if (front == rear) return queue_full();
    queue[rear] = item;
    }
    

• Delete
  • Increment “front” by “1” in a clockwise direction;
  • 
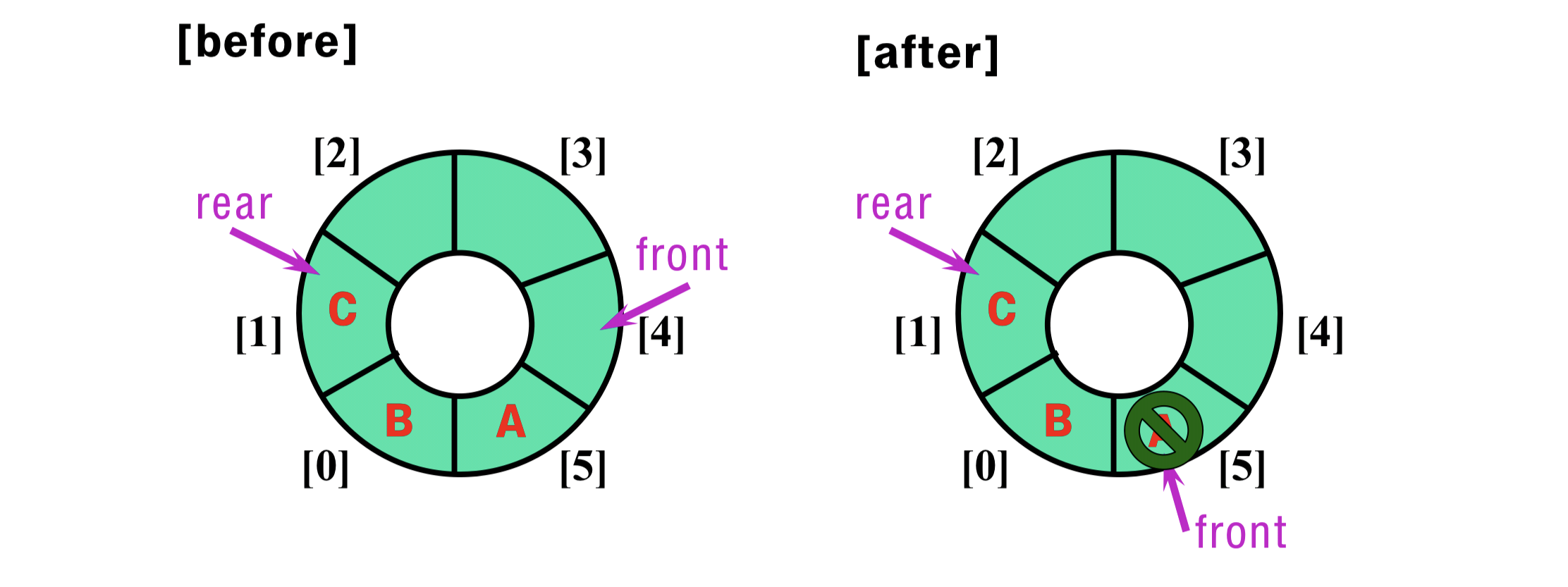
  • if “front” reaches the end of queue, reset “front” by “0”
  • Condition of Queue Empty : front == rear

    Delete(){
    if (front == rear) return queue_empty();
    front = (front + 1) % MAX_Q_SIZE;
    item = queue[front]
    }
    

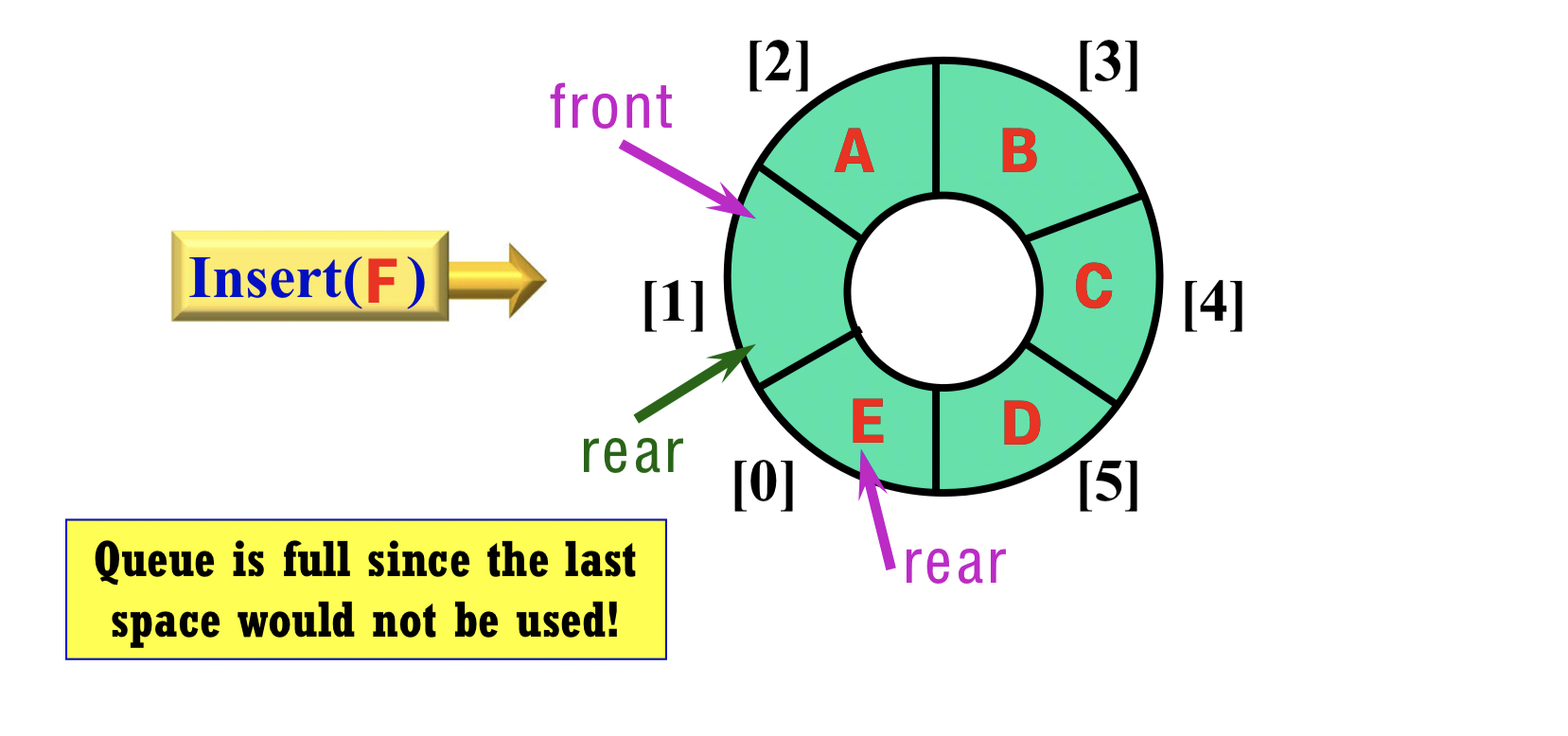
3.5 Problem

• full and empty condition is the same!
• Solution
  • option1 :
    • Only permit MAX_Q_SIZE -1 elements; (one space in a queue is not used)
    • But, at rear == front, reset the rear with the prior position (i.e., rear = rear -1)
    • 
  • option2 : A Boolean variable (e.g: Tag) is additionally used
    • After insert/ delete, set the Tag to true/false
    • Queue is empty if (front == rear) && ! Tag
    • Queue is full if (front == rear) && Tag

3.6 Queue: Applications

• Job Processing (printer, CPU processor)
• Data Buffers
• Waiting times of customers at a public phone
• Deciding number of cashiers (tellers) at super market (bank)
• Traffic Analysis